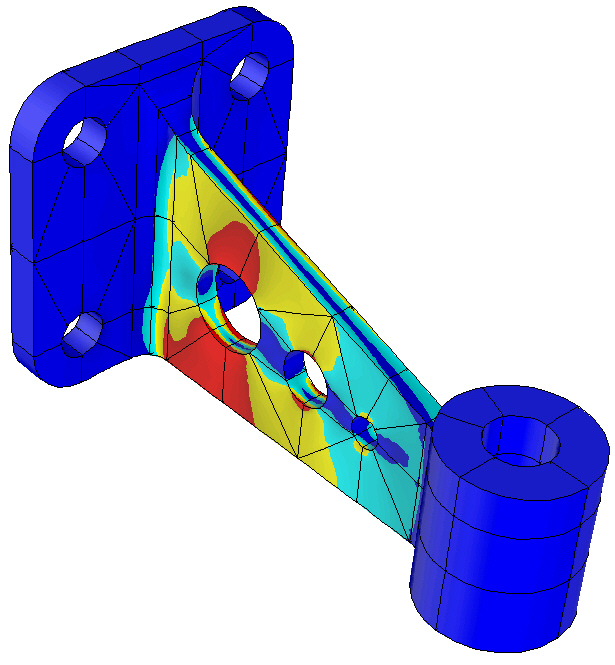
Problems in engineering often require the solution of large systems of complicated equations (called partial differential equations, PDEs) to find the quantities of interest. For instance, if a machine component in your automobile is being designed, engineers need to know how strong to make it, so that it can withstand the stresses that it will be subjected to when it is in use. For this, they need to first find the maximum stress that the part will have to tolerate, and where this maximum will occur, so that they can incorporate the right amount of material there. It is important to get an accurate idea of this stress, because otherwise, they might end up with a component that is not strong enough (which is dangerous) or too strong (which is wasteful in terms of weight/efficiency). The bracket in the above picture shows a typical stress distribution with the red denoting regions of highest stress.
Building the part and testing it mechanically is the expensive way to tackle this problem. But before this stage, the design process usually involves several computer simulations of the component. The component is input into engineering computer codes and various loads are imposed, on its volume, surface and boundary to simulate the ones that would act on it in real life. The required stresses can be calculated from these loads, but only through a system of PDEs. Unlike algebraic equations in unknowns x, y, z that one might encounter in high school (like 3x+4y-9z=8), PDEs relate the rates at which the unknowns are changing to the loads and to each other. They are generally not solvable using paper or pencil, but must be approximated on a computer using mathematical algorithms. The field of (applied) mathematics that deals with the construction of such algorithms and the characterization of their mathematical properties is called Numerical Analysis . (The field has a broader scope than just PDEs – for instance, it comes up in the computer modeling of such diverse phenomenon as weather to the stock market.)
One of the most important benefits that comes from mathematicians analyzing such algorithms is that they can help engineers predict whether the approximations obtained are accurate or not, i.e. they can help estimate the error that comes from approximating the true answer by the calculated one. Failure to do so can result in disastrous results, the best-known of which is the $700 million loss from The sinking of the Sleipner A offshore platform explained on Professor Doug Arnold’s homepage.